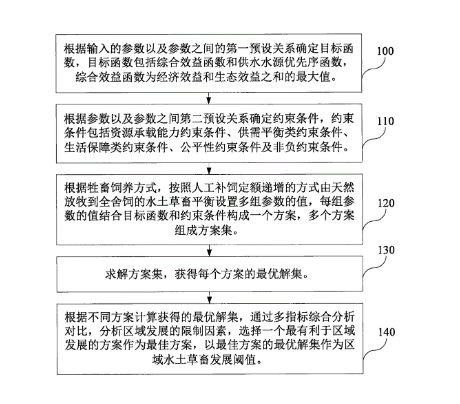
1.一种牧区水土草畜平衡模型的计算方法，其特征在于，所述方法包括： 根据输入的参数以及所述参数之间的第一预设关系确定目标函数，所述目标函数包括综合效益函数和供水水源优先序函数，所述综合效益函数为经济效益和生态效益之和的最大值； 根据所述参数以及所述参数之间的第二预设关系确定约束条件，所述约束条件包括资源承载能力约束条件、供需平衡类约束条件、生活保障类约束条件、公平性约束条件及非负约束条件； 根据牲畜饲养方式，按照人工补饲定额递增的方式由天然放牧到全舍饲的水土草畜平衡设置多组所述参数的值，每组参数的值结合所述目标函数和约束条件构成一个方案，多个所述方案组成方案集； 求解所述方案集，获得每个所述方案的最优解集； 根据不同所述方案计算获得的最优解集，通过多指标综合分析对比，分析区域发展的限制因素，选择一个最有利于区域发展的所述方案作为最佳方案，以所述最佳方案的最优解集作为区域水土草畜发展阈值； 其中，求解所述方案集，获得每个所述方案的最优解集包括： 将每个所述方案的所述目标函数的解对应到[0，1]区间上，获得所有解的编码形式，所述解的编码形式称为个体； 随机生成多个所述个体，对每个所述个体进行合理性检验，保留满足所述约束条件的个体作为初始个体，多个所述初始个体组成初始种群； 计算所述初始种群中每个所述初始个体的适应度； 以所述初始种群中的初始个体作为父代个体，并根据所述父代个体的适应度生成相应的子代个体； 将第一代进化产生的适应度最靠前的n个子代个体的集合作为现有非劣解集保存，以后对于每一代进化所产生的最好的n个子代个体与所述现有非劣解集中的各解逐一进行比较，保留优解替换劣解，获得非劣解集； 当进化次数达到预设进化次数，且迭代次数也达到预设的迭代次数时，保留的经过替换得到的所述非劣解集，作为最优解集； 其中，根据以下公式确定所述综合效益函数： fc＝Max(OBE+OBEN) 式中，fc为所述综合效益函数，OBE为所述经济效益，OBEN为所述生态效益； 所述经济效益OBE通过以下公式确定： OBE＝ANB+INB 式中，ANB为农牧业净效益，INB为非农牧业净效益； 所述农牧业净效益通过以下公式确定： ANB＝ANBA+ANBL 式中，ANBA为种植业灌溉净效益，ANBL为牲畜饲养净效益； 所述种植业灌溉净效益通过以下公式确定：  式中，ACA(f)为f类种植作物的灌溉面积，P(f)、Y(f)和C(f)分别为f类种植作物的单价、亩均产量和种植成本，WP为水价，WN(f)为f类种植作物的毛灌溉定额； 所述牲畜饲养净效益通过以下公式确定：  式中，LSL为牲畜饲养量，即标准羊单位，P(l)和Y(l)分别为牲畜标准羊单位第1类产品的产量和单价，ω为牲畜出栏率，C为牲畜标准羊单位的成本，WNL为牲畜标准羊单位饮水定额； 所述非农牧业净效益INB以工业用水净效益表示为： INB＝IAV·ψ·δ 式中，IAV为工业增加值，ψ为工业净值占总产值的比例，δ为工业用水效益分摊系数； 所述生态效益OBEN通过以下公式确定：  式中，ANAk为第k类天然牧场利用面积，OBEND为动态草原生态服务价值，AREA为天然牧场可利用面积，ξ(k)为第k类天然牧场对应采食率下的折算系数； 所述动态草原生态服务价值通过以下公式确定： OBEND＝l·r·OBENS 式中，l为相对支付意愿，r为天然草原资源稀缺程度，可按照天然草原退化程度取值，取值范围[0，1]，OBENS为静态草原生态服务价值； 所述相对支付意愿l表达式为：  式中，L为所述相对支付意愿l的最大值，表示极富阶段的支付意愿，取值为1，t为时间变量，表示社会经济发展阶段，a、b为常数，取值为1，e为自然对数； 其中，所述时间变量t表达式为：  式中，En为恩格尔系数； 所述静态草原生态服务价值通过以下公式确定：  式中，AREAi为i类天然草原面积，VPAi为i类天然草原天然状态下的草原生态服务价值单价； 根据以下公式确定所述供水水源优先序函数：  式中，fw为所述供水水源优先序函数，OBW为供水水源优先序数，αi和βj分别为i行业供水权重系数和j水源的供水优先序系数，WSL(i，j，t)为t时段i行业j水源的供水量； 所述资源承载能力约束条件包括水资源承载能力约束条件、草地资源承载能力约束条件和土地资源承载能力约束条件； 所述水资源承载能力约束条件表达式为：  式中，WSG(t)max为t时段供水工程最大供水能力，WLL(j，t)为t时段j水源的可利用量，WTL(t)为t时段外调水量，WUI为区域用水总量控制指标； 所述草地资源承载能力约束条件表达式为： LSL·LNk·Tk≤ANAk·NCLk LSL·ILNl·Tl≤IGAl·CLl  式中，LNk为k类天然牧场羊单位采食定额，Tk为k类天然牧场的饲养天数，NCLk为k类天然牧场的干草产量，ILNl为l类灌溉人工草地羊单位采食定额，Tl为l类灌溉草地的饲养天数，IGAl为l类灌溉草地的面积，CLl为l类灌溉草地的干草产量； 所述土地资源承载能力约束条件表达式为：  式中，ACA为种植作物灌溉面积，FCAm为第m类粮食作物灌溉面积，ECAn为第n类经济作物灌溉面积，AFL为可利用耕地面积，R为复种指数； 所述供需平衡类约束条件包括水资源供需平衡约束条件和饲草料供需平衡约束条件，所述水资源供需平衡约束条件的表达式为：  WRL(i，t)＝EI(i，t)·WN(i，t) 式中，WRL(i，t)为t时段第i类行业的需水量，EI(i，t)为t时段第i类行业的经济指标，WN(i，t)为t时段第i类行业的需水定额； 所述饲草料供需平衡约束条件的表达式为： LSL·ILNl·Tl＝IGAl·CLl； 所述生活保障类约束条件包括粮食作物最低约束条件和牲畜饲料基本数约束条件；所述粮食作物最低约束条件的表达式为：  式中，FCDm为第m类粮食作物单位面积产量，PGD为人均粮食需求量，POP为人口总数； 所述牲畜饲料基本数约束条件的表达式为： LSL≥LSLmin 式中，LSLmin为牲畜基础饲养数量； 所述公平性约束条件的表达式为： EImin(i，t)≤EI(i，t)≤EImax(i，t) WSLmin(i，j，t)≤WSL(i，j，t)≤WSLmax(i，j，t) 式中，EImin(i，t)为t时段i行业经济指标的最低限，EImax(i，t)为t时段i行业经济指标的最高限，WSLmin(i，j，t)为t时段i行业j水源供水量的最低限，WSLmax(i，j，t)为t时段i行业j水源供水量的最高限。

2.如权利要求1所述的方法，其特征在于，当所述迭代次数未达到所述预设的迭代次数时，重新进行下一次迭代，直到所述迭代次数达到所述预设的迭代次数为止。

3.如权利要求1所述的方法，其特征在于，通过以下公式确定所述解的编码形式： x(j)＝a(j)+y(j)[(b(j)-a(j))] (j＝1，2，…，p) 式中，[a(j)，b(j)]为预先设置的第j个优化变量x(j)的初始变化区间，y(j)为x(j)对应到[0，1]上的实数，称其为基因，所述编码形式表示为(y(1)，y(2)，…，y(p))，其中所述优化变量x(j)为每个方案对应的所述目标函数的解。

4.如权利要求1所述的方法，其特征在于，通过以下公式确定所述初始个体的适应度：   式中：Rt(i)为所述初始种群中第i个个体对目标函数t的排序序号，Ft(i)为所述初始种群中第i个个体对目标t所得的适应度，F(i)为所述初始种群中第i个个体对全部目标函数的综合适应度，k为(1，2)内的常数，用于加大表现最优的个体适应度，获得更多的参与机会，n为所述目标函数个数，N为所述初始种群中个体的个数。

5.一种牧区水土草畜平衡模型的计算系统，其特征在于，所述系统包括： 目标函数确定模块，用于根据输入的参数以及所述参数之间的第一预设关系确定目标函数，所述目标函数包括综合效益函数和供水水源优先序函数，所述综合效益函数为经济效益和生态效益之和的最大值； 约束条件确定模块，用于根据所述参数以及所述参数之间的第二预设关系确定约束条件，所述约束条件包括资源承载能力约束条件、供需平衡类约束条件、生活保障类约束条件、公平性约束条件及非负约束条件； 方案集设置模块，用于根据牲畜饲养方式，按照人工补饲定额递增的方式由天然放牧到全舍饲的水土草畜平衡设置多组所述参数的值，每组参数的值结合所述目标函数和约束条件构成一个方案，多个所述方案组成方案集； 方案集求解模块，用于求解所述方案集，获得每个方案的最优解集； 最佳方案确定模块，用于根据不同方案计算获得的最优解集，通过多指标综合分析对比，分析区域发展的限制因素，选择一个最有利于区域发展的方案作为最佳方案，以最佳方案的最优解集作为区域水土草畜发展阈值； 其中，所述方案集求解模块包括： 个体编码子模块，用于将每个所述方案的所述目标函数的解对应到[0，1]区间上，获得所有解的编码形式，所述解的编码形式称为个体； 种群生成和初始化子模块，用于随机生成多个所述个体，对每个所述个体进行合理性检验，保留满足所述约束条件的个体作为初始个体，多个所述初始个体组成初始种群； 适应度计算子模块，用于计算所述初始种群中每个所述初始个体的适应度； 子代个体生成子模块，用于以所述初始种群中的初始个体作为父代个体，并根据所述父代个体的适应度生成相应的子代个体； 非劣解集计算子模块，用于将第一代进化产生的适应度最靠前的n个子代个体的集合作为现有非劣解集保存，以后对于每一代进化所产生的最好的n个子代个体与所述现有非劣解集中的各解逐一进行比较，保留优解替换劣解，获得非劣解集； 最优解集计算子模块，用于当进化次数达到预设进化次数时判断迭代次数是否达到预设的迭代次数，若是，保留的经过替换得到的所述非劣解集，作为最优解集；否则重新进行下一次迭代，直到迭代次数达到预设的迭代次数为止；当获得一个方案的最优解集后，重复进化和迭代步骤计算下一个方案的最优解集； 其中，根据以下公式确定所述综合效益函数： fc＝Max(OBE+OBEN) 式中，fc为所述综合效益函数，OBE为所述经济效益，OBEN为所述生态效益； 所述经济效益OBE通过以下公式确定： OBE＝ANB+INB 式中，ANB为农牧业净效益，INB为非农牧业净效益； 所述农牧业净效益通过以下公式确定： ANB＝ANBA+ANBL 式中，ANBA为种植业灌溉净效益，ANBL为牲畜饲养净效益； 所述种植业灌溉净效益通过以下公式确定：  式中，ACA(f)为f类种植作物的灌溉面积，P(f)、Y(f)和C(f)分别为f类种植作物的单价、亩均产量和种植成本，WP为水价，WN(f)为f类种植作物的毛灌溉定额； 所述牲畜饲养净效益通过以下公式确定：  式中，LSL为牲畜饲养量，即标准羊单位，P(l)和Y(l)分别为牲畜标准羊单位第1类产品的产量和单价，ω为牲畜出栏率，C为牲畜标准羊单位的成本，WNL为牲畜标准羊单位饮水定额； 所述非农牧业净效益INB以工业用水净效益表示为： INB＝IAV·ψ·δ 式中，IAV为工业增加值，ψ为工业净值占总产值的比例，δ为工业用水效益分摊系数； 所述生态效益OBEN通过以下公式确定：  式中，ANAk为第k类天然牧场利用面积，OBEND为动态草原生态服务价值，AREA为天然牧场可利用面积，ξ(k)为第k类天然牧场对应采食率下的折算系数； 所述动态草原生态服务价值通过以下公式确定： OBEND＝l·r·OBENS 式中，l为相对支付意愿，r为天然草原资源稀缺程度，可按照天然草原退化程度取值，取值范围[0，1]，OBENS为静态草原生态服务价值； 所述相对支付意愿l表达式为：  式中，L为所述相对支付意愿l的最大值，表示极富阶段的支付意愿，取值为1，t为时间变量，表示社会经济发展阶段，a、b为常数，取值为1，e为自然对数； 其中，所述时间变量t表达式为：  式中，En为恩格尔系数； 所述静态草原生态服务价值通过以下公式确定：  式中，AREAi为i类天然草原面积，VPAi为i类天然草原天然状态下的草原生态服务价值单价； 根据以下公式确定所述供水水源优先序函数：  式中，fw为所述供水水源优先序函数，OBW为供水水源优先序数，αi和βj分别为i行业供水权重系数和j水源的供水优先序系数，WSL(i，j，t)为t时段i行业j水源的供水量； 所述资源承载能力约束条件包括水资源承载能力约束条件、草地资源承载能力约束条件和土地资源承载能力约束条件； 所述水资源承载能力约束条件表达式为：  式中，WSG(t)max为t时段供水工程最大供水能力，WLL(j，t)为t时段j水源的可利用量，WTL(t)为t时段外调水量，WUI为区域用水总量控制指标； 所述草地资源承载能力约束条件表达式为： LSL·LNk·Tk≤ANAk·NCLk LSL·ILNl·Tl≤IGAl·CLl  式中，LNk为k类天然牧场羊单位采食定额，Tk为k类天然牧场的饲养天数，NCLk为k类天然牧场的干草产量，ILNl为l类灌溉人工草地羊单位采食定额，Tl为l类灌溉草地的饲养天数，IGAl为l类灌溉草地的面积，CLl为l类灌溉草地的干草产量； 所述土地资源承载能力约束条件表达式为：  式中，ACA为种植作物灌溉面积，FCAm为第m类粮食作物灌溉面积，ECAn为第n类经济作物灌溉面积，AFL为可利用耕地面积，R为复种指数； 所述供需平衡类约束条件包括水资源供需平衡约束条件和饲草料供需平衡约束条件，所述水资源供需平衡约束条件的表达式为：  WRL(i，t)＝EI(i，t)·WN(i，t) 式中，WRL(i，t)为t时段第i类行业的需水量，EI(i，t)为t时段第i类行业的经济指标，WN(i，t)为t时段第i类行业的需水定额； 所述饲草料供需平衡约束条件的表达式为： LSL·ILNl·Tl＝IGAl·CLl； 所述生活保障类约束条件包括粮食作物最低约束条件和牲畜饲料基本数约束条件；所述粮食作物最低约束条件的表达式为：  式中，FCDm为第m类粮食作物单位面积产量，PGD为人均粮食需求量，POP为人口总数； 所述牲畜饲料基本数约束条件的表达式为： LSL≥LSLmin 式中，LSLmin为牲畜基础饲养数量； 所述公平性约束条件的表达式为： EImin(i，t)≤EI(i，t)≤EImax(i，t) WSLmin(i，j，t)≤WSL(i，j，t)≤WSLmax(i，j，t) 式中，EImin(i，t)为t时段i行业经济指标的最低限，EImax(i，t)为t时段i行业经济指标的最高限，WSLmin(i，j，t)为t时段i行业j水源供水量的最低限，WSLmax(i，j，t)为t时段i行业j水源供水量的最高限。

请联系平台

请联系平台